Answer:
The length of the hypotenuse is
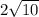 ≅ 6.325
≅ 6.325
Explanation:
∵ A right angle is formed by the x-axis, y-axis and the line y = -3x + 6
∴ The line intersected the x-axis at point (x, 0)
→ To find x substitute y in the equation by 0
∵ 0 = -3x + 6
→ Add 3x to both sides
∴ 0 + 3x = -3x + 3x + 6
∴ 3x = 6
→ Divide both sides by 3
∵
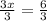
∴ x = 2
∴ The line intersected the x-axis at point (2, 0)
∵ The line intersected the y-axis at point (0, y)
→ Substitute x in the equation by 0 to find y
∴ y = -3(0) + 6
∵ y = 0 + 6
∴ y = 6
∴ The line intersected the xyaxis at point (0, 6)
∵ The endpoints of the hypotenuse are (2, 0) and (0, 6)
→ Use the rule of the distance d =
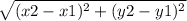 to find it
to find it
∵ x1 = 2 and y1 = 0
∵ x2 = 0 and y2 = 6
∴ h =

∴ The length of the hypotenuse is
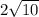 ≅ 6.325
≅ 6.325
The attached figure for more understanding