Answer:
The expected number of boys a family might have is 2.5.
Explanation:
Let X denote the number of boys in a family with 5 children.
The probability of a boy is, p = 0.50.
The child can either be a by or a girl independently.
The random variable X follows a binomial distribution with parameters n = 5 and p = 0.50.
The probability mass function is:

Compute the expected number of boys a family might have as follows:
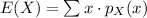
x p (x) x · p (x)
0
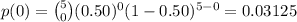
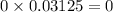
1
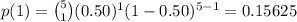

2
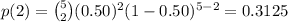
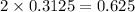
3
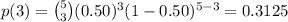
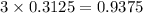
4
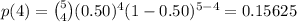

5
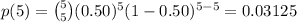
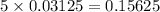
Then,
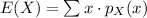

Thus, the expected number of boys a family might have is 2.5.