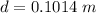Answer:
a
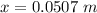
b
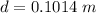
Step-by-step explanation:
From the question we are told that
The spring constant is
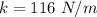
The mass of the block is
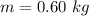
Considering question a
Generally the weight of the block is mathematically represented as
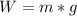
=>
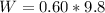
=>

Generally the force exerted on the spring is mathematically represented as
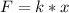
At equilibrium

=>
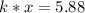
=>
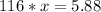
=>
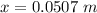
Considering question b
Generally the energy stored in the spring is mathematically represented as
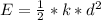
Now the potential energy of the block before it is drooped is mathematically represented as
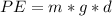
Generally from the law of energy conservation we have that

=>
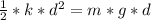
=>
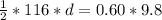
=>