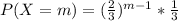Question

In a jar, there is a green, a blue, and a red marble. You draw (with replacement) a marble from the jar until you get the green marble. What is the probability that you draw exactly m times, where m is a positive integer?

Answer 1

The value is
`P( X = m ) = ((2)/(3) )^(m-1 ) * (1)/(3)`

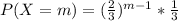
Explanation:

From question we are told that

The number of types of marbles present jar is n = 3

Generally the probability of drawing a green marble is

`P(g) = (1)/(3)`

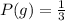
Generally the probability of drawing a marble that is not green is

`P(g') = 1 - (1)/(3) = (2)/(3)`

From the question we are told that there will be continuous drawing of marbles from the jar (in such a way that after each marble is drawn it is being replaced) until a green marble drawn

Let m be the number of times marbles has been drawn when a green marble was gotten

it then means that for m - 1 times the marbles where drawn a green marble was not obtain.

Generally the probability drawing m times is mathematically is mathematically represented as

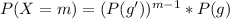
`P( X = m ) = (P(g'))^(m-1 ) * P(g)`

=>
`P( X = m ) = ((2)/(3) )^(m-1 ) * (1)/(3)`