Question

How many pounds a statistician can bench press is normally distributed with a mean of 139 and standard deviation of 46. If Scott can bench 145 pounds, approximately what percentage of statisticians can bench more than Scott

Answer 1

The percentage is
`P(X > 145 ) = 44.811\%`

Explanation:

From the question we are told that

The mean is
`\mu = 139`

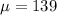
The standard deviation is
`\sigma = 46`

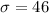
The weight Scott can bench is x = 145 pounds

Generally the percentage of statisticians that can bench more than Scott is mathematically represented as

`P(X > x ) = P((X - \mu )/(\sigma ) > (x- 139 )/(46 ) )`

=>
`P(X > 145 ) = P((X - \mu )/(\sigma ) > (145 - 139 )/(46 ) )`

`(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )`

`P(X > 145 ) = P(Z > 0.13043)`

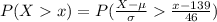
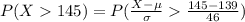
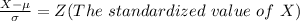
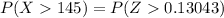
From the z table

The area under the normal curve to the right corresponding to 0.13043 is

`P(Z > 0.13043) = 0.44811`

=>
`P(X > 145 ) = 0.44811`

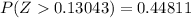
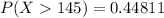
Converting to percentage

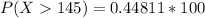
`P(X > 145 ) = 0.44811 * 100`

=>
`P(X > 145 ) = 44.811\%`