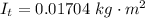Question

Model a real bowling ball as a 0.196-m-diameter core with mass 1.6 kg plus a thin 1.6 kg shell with diameter 0.206 m (the average of the inner and outer diameters). What is the total moment of inertia

Answer 1

The total moment of inertia is
`I_ t =0.01704 \ kg \cdot m^2`

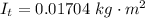
Step-by-step explanation:

From the question we are told that

The diameter of the core is
`d = 0.196 \ m`

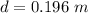
The mass of the core is
`m_c = 1.6 \ kg`

The mass of the shell is
`m_s = 1.6 \ kg`

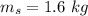
The diameter of the shell is
`d_s = 0.206 \ m`

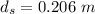
Generally the radius of the core is

`r_c = (d)/(2)`

=>
`r_c = ( 0.196 )/(2)`

=>
`r_c = 0.098 \ m`

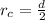
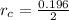
Generally the radius of the shell is

`r_s = (d_s)/(2)`

=>
`r_s = ( 0.206 )/(2)`

=>
`r_s = 0.103 \ m`

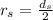
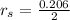
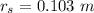
Generally the total moment of inertia is mathematically represented as

`I_ t = I_c + I_s`

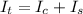
Here
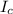`I_c` is the moment of inertia of the core which is mathematically represented as

`I_c = (2)/(5) * m_c * r_c^2`

=>
`I_c = (2)/(5) * 1.60 *(0.098)^2`

=>
`I_c = 0.01024 \ kg \cdot m^2`

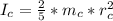
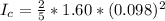
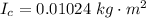
and
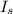`I_s` is the moment of inertia of the shell which is mathematically represented as

`I_s = (2)/(5) *m_s * r_s^2`

=>
`I_s = (2)/(5) * 1.60 *(0.103)^2`

=>
`I_s = 0.0068 \ kg \cdot m^2`

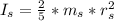
So

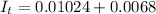
`I_ t = 0.01024 + 0.0068`

=>
`I_ t =0.01704 \ kg \cdot m^2`