Question

The nth term of a sequence is represented by
`( 2n^3+25n^2+32n-15)/(6n^4+2n^3-11n^2-2n+17)`

What is the limit of the nth term as x becomes increasingly large?

A. 0
B. 1/3
C. 3
D. Limit does not exist.

Answer 1

I think that the possible answer is 3

Answer 2

A) 0

Step-by-step explanation:

`\sf \lim _(x\to \infty )\left((2n^3+25n^2+32n-15)/(6n^4+2n^3-11n^2-2n+17)\right)`

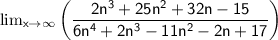
1) Limit does not exist when the numerator is bigger.

2) Limit is zero when the denominator is bigger.

3) Limit is the ratio of coefficients when both powers are equal.

Here, the denominator have a power of 4, bigger than the numerator.

Hence, the limit of the nth term is 0.