Question

Segment DG has endpoints D(-7,-4) and G(8,1). Find the coordinates of J such that the ratio of DJ:JG is 2:3

Answer 1

Given:

DG has endpoints D(-7,-4) and G(8,1).

DJ:JG = 2:3

To find:

The coordinates of J.

Solution:

We have,

DJ:JG = 2:3

It means, point J divides the segment DG is 2:3.

Section formula: If a point divides a lines segment with end point
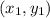`(x_1,y_1)` and
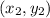`(x_2,y_2)` in m:n, then coordinates of point are

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

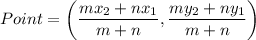
Using section formula, the coordinate of J are

`J=\left((2(8)+3(-7))/(2+3),(2(1)+3(-4))/(2+3)\right)`

`J=\left((16-21)/(5),(2-12)/(5)\right)`

`J=\left((-5)/(5),(-10)/(5)\right)`

`J=\left(-1,-2\right)`

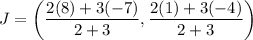
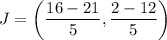
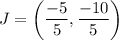
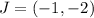
Therefore, the coordinates of J are (-1,-2).