The missing values in the given question is shown below.
A tobacco company claims that the nicotine content of its "light" cigarettes has a mean of 1.5 milligrams and a standard deviation of 0.52 milligrams. What is the probability that 50 randomly selected light cigarettes from this company will have a total combined nicotine content of 81 milligrams or less, assuming the company's claims to be true? Carry your intermediate computations to at least four decimal places. Report your result to at least three decimal places.
Answer:
P(x ≤ 1.62) = 0.949 to three decimal places.
Explanation:
From the question; given that:
The population mean = 1.5
The standard deviation = 0.52
The sample size n = 50
The sample mean
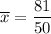 = 1.62
= 1.62
Hence; we can calculate the required probability as:
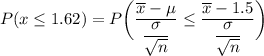

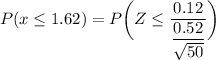
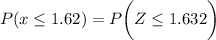
From z - tables;
P(x ≤ 1.62) = 0.9486
P(x ≤ 1.62) = 0.949 to three decimal places.