Answer:
a
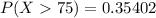
b
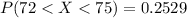
c

Explanation:
From the question we are told that
The population mean is
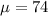
The population standard deviation is
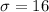
Considering question a
The sample size is n = 36
Generally the standard error of mean is mathematically represented as

=>
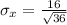
=>
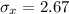
Generally the probability that a random sample of size 36 yielding a sample mean of 75 or more is mathematically represented as
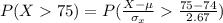
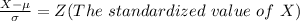

From the z table the area under the normal curve representing 0.3745 to the right is

=>
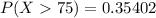
Considering question b
The sample size is n = 104
Generally the standard error of mean is mathematically represented as

=>
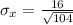
=>
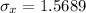
Generally the probability that a random sample of size 104 yielding a sample mean between 72 and 75 is mathematically represented as
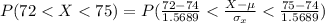
=>
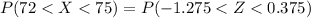
=>
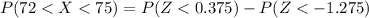
From the z table the area under the normal curve representing -1.275 to to the left is
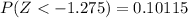
=>
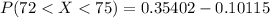
=>
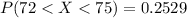
Considering question c
The sample size is n = 217
Generally the standard error of mean is mathematically represented as

=>
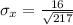
=>
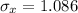
Generally the probability that a random sample of size 217 yielding a sample mean of less than 74.7 is mathematically represented as
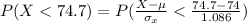
=>
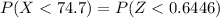
From the z table the area under the normal curve representing 0.6446 to to the left is
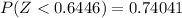
=>
