Question

Uninsured: It is estimated that 19% of all adults in the U.S. are uninsured. We will assume this is accurate. You take a random sample of 200 adults seen by a certain clinic and find that 28 (about 14%) are uninsured. (a) Assume the quoted value of 19% for uninsured adults is accurate. What what is the mean number of uninsured adults in all random samples of size 200

Answer 1

Complete Question

Uninsured: It is estimated that 19% of all adults in the U.S. are uninsured, we will assume this is accurate. You take a random sample of 200 adults seen by a certain clinic and find that 50 (about 14%) are uninsured. (a) Assume the quoted value of 19% for uninsured adults is accurate, what what is the mean number of uninsured adults in all random samples of size 200? Round your answer to one decimal place.

(b) What is the standard deviation? Round your answer to one decimal place

(c) In your survey you found 50 of the 200 U.S. adults are uninsured. With respect to the mean and standard deviation found in parts (a) & (b) ured adults

Answer:

a

`\mu = 38`

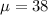
b

`\sigma = 5.5`

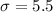
c

`z = 2.1818`

Explanation:

From the question we are told the

The percentage of uninsured U.S adults is p = 0.19

The sample size is n = 200

Generally the distribution of number of uninsured U.S adults follows a binomial distribution

i.e

`X  \~ \ \ \  B(n , p)`

Here X denotes the number of uninsured U.S adults

Generally the mean number of uninsured U.S adults is mathematically evaluated as

`\mu = n * p`

=>
`\mu = 200 * 0.19`

=>
`\mu = 38`

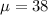
Generally the standard deviation is mathematically represented as

`\sigma = √(n * p * (1 - p))`

`\sigma = √(200 * 0.19 * (1 - 0.19 ))`

`\sigma = 5.5`

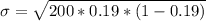
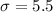
Generally the z-score is mathematically represented as

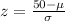
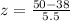
`z = (50 - \mu )/(\sigma )`

=>
`z = (50 - 38 )/(5.5 )`

=>
`z = 2.1818`