Question

Match each function with the graph of its inverse functions.

Answer 1

Explanation:

1). f(x) = 5x - 1

Convert the function into the equation,

y = 5x - 1

Substitute 'x' by 'y' and 'y' by 'x',

x = 5y - 1

Solve the equation for y,

y =
`(1)/(5)x+(1)/(5)`

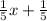
So the inverse function is,

`f^(-1)(x)=(1)/(5)x+(1)/(5)`

Y-intercept of the function is
`(1)/(5)`

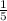
Therefore, graph (2) is the answer.

2). f(x) =
`(1)/(5)x`

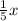
Inverse of this function will be,

`f^(-1)(x)=5x`

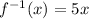
So the line of this function will pass through the origin.

Graph (3) will be the answer.

3). f(x) = x - 5

`f^(-1)(x)=x+5`

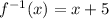
Graph having y-intercept = 5 will be the answer.

Option (4) will be the graph of the given inverse function.

4). f(x) = 7x + 1

Inverse of this function will be,

`f^(-1)x=(1)/(7)(x-1)`

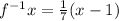
Graph with Y-intercept =
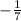`-(1)/(7)` (Negative y-intercept) will be the answer.

Option (1) will be the answer.