Question

Urgent***
Determine the zeros, sign and extreme values of the function y = -x³ + 8x²-16x.​

Answer 1

Explanation:

To find extreme values, take the first derivative

`y = - 3 {x}^(2) + 16x - 16`

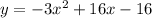
Solve the equation for x.

`x = ( - 16 + √(256 - 192) )/( - 6)`

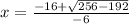
or

`x = ( - 16 - √(256 - 192) )/( - 6)`

`x = ( - 16 + √(64) )/( - 6)`

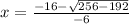
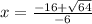
or

`x = ( - 16 - √(64) )/( - 6)`

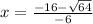
We then get

`x = (4)/(3)`

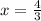
or

`x = 4`

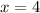
So our extreme values occur at x=4/3 and x=4

Zeroes:

`- {x}^(3) + 8 {x}^(2) - 16x`

`- x( {x}^(2) - 8x + 16)`

`- x(x - 4) {}^(2)`

`- x = 0`

`(x - 4) {}^(2) = 0`

`x = 4`

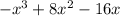
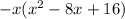
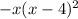
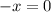
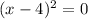
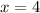
So we have a double root at 4, and a root of 0. We have two positive roots and one non negative root

End behavior:

Since we have a negative leading coefficient and a odd degree, as x becomes more positive, y will become negative and as x becomes more negative, y will become positive.