Question

Give the general solution in degrees and radians. 9) 8cosØ = 4​

Answer 1

Hi Student!

The first step that we need to take before solving this problem is understand what we need to do and what information we are given to do that. So first they are asking for us to determine the solution (or find theta) in both degrees and radians. The information that is given to us is the equation
`8* cos (\theta) = 4`.

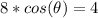After completing the initial step, the next step is to actually start solving the equation for the unknown which in this case is theta or the angle.

Divide both sides by 8

• 
  `8* cos (\theta) = 4`

• 
  `(8* cos (\theta))/(8) = (4)/(8)`

• 
  `cos (\theta) = (1)/(2)`

• 
  `cos (\theta) = 0.5`

Multiply by the inverse of cos

• 
  `cos^(-1)(cos (\theta)) = cos^(-1)(0.5)`

• 
  `\theta = cos^(-1)(0.5)`

• 
  `\theta = 60`

After solving for the unknown or theta, we were able to determine that the solution for our equation is 60 degrees. Now we can move onto the final step which is to convert our answer to radians to complete the final part of the problem statement.

We can convert from degrees to radians by multiplying by π/180 which would get rid of degrees and give us radians.

Plug in the values

• 
  `degrees*(\pi )/(180\ degrees)`

• 
  `60\ degrees*(\pi )/(180\ degrees)`

Simplify the expression

• 
  `(\pi\ *\ 60\ degrees )/(180\ degrees)`

• 
  `(\pi)/(3)`

Therefore, our final answer is that our solution in degrees is 60 degrees and our solution in radians is π/3.