Question

The college that Dora attends is selling tickets to the annual

battle of the bands competition. On the first day of ticket sales
the college sold 3 student tickets and 3 adult tickets for a total
of $69. The school took in $91 on the second day by selling 5
student tickets and 3 adults tickets. Use elimination to solve
the system of linear equations and determine the price each
student ticket, x and each adult ticket, y. Write your answer as
an ordered pair (x,y).

Answer 1

(11,12)

Explanation:

Answer 2

The solution of the system of equations is (11, 12)

Explanation:

∵ The price of each student ticket is $x

∵ The price of each adult ticket is $y

∵ They sold 3 student tickets and 3 adult tickets for a total of $69

∴ 3x + 3y = 69 ⇒ (1)

∵ they sold 5 student tickets and 3 adults tickets for a total of $91

∴ 5x + 3y = 91 ⇒ (2)

Let us solve the system of equations using the elimination method

→ Subtract equation (1) from equation (2)

∵ (5x - 3x) + (3y - 3y) = (91 - 69)

∴ 2x + 0 = 22

∴ 2x = 22

→ Divide both sides by 2 to find x

∵
`(2x)/(2)=(22)/(2)`

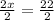
∴ x = 11

→ Substitute the value of x in equation (1) or (2) to find y

∵ 3(11) + 3y = 69

∴ 33 + 3y = 69

→ Subtract 33 from both sides

∵ 33 - 33 + 3y = 69 - 33

∴ 3y = 36

→ Divide both sides by 3

∵
`(3y)/(3)=(36)/(3)`

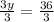
∴ y = 12

∴ The solution of the system of equations is (11, 12)