Question

The mean daily rainfall in Los Angeles in December is 0.05 inches with a standard deviation of 0.02 inches. What is the probability that

the total rainfall in Los Angeles for 37 randomly selected December days (possibly over several years) will not exceed 2 inches?
Carry your intermediate computations to at least four decimal places. Report your result to at least three decimal places.

Answer 1

The probability that the total rainfall will not exceed 2 inches is 0.8907.

Explanation:

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sum of values of X, i.e ∑X, will be approximately normally distributed.

Then, the mean of the distribution of the sum of values of X is given by,

`\mu_(x)=n\mu`

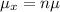
And the standard deviation of the distribution of the sum of values of X is given by,

`\sigma_(x)=√(n)\sigma`

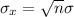
As the sample size is large, i.e. n = 37 > 30, the Central Limit Theorem can be used to approximate the sampling distribution of sample mean daily rainfall in Los Angeles.

Compute the probability that the total rainfall will not exceed 2 inches as follows:

`P(\sum X\leq 2)=P((\sum X-n\mu)/(√(n)\sigma)\leq (2-(37* 0.05))/(√(37)* 0.02))\\\\=P(Z<1.23)\\\\=0.89065\\\\\approx 0.8907`

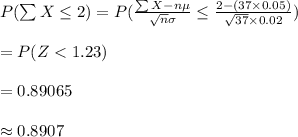
Thus, the probability that the total rainfall will not exceed 2 inches is 0.8907.