Answer:
x = 3
Explanation:
using the sine ratio in right triangle ABC and the exact value
sin45° =
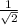 , then
, then
sin45° =
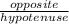 =
=
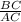 =
=
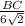 =
=
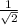 ( cross- multiply )
( cross- multiply )
BC ×
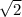 = 6
= 6
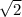 ( divide both sides by
( divide both sides by
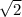 )
)
BC = 6
using the cosine ratio in right triangle BCD and the exact value
cos60° =
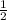 , then
, then
cos60° =
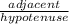 =
=
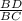 =
=
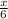 =
=
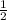 ( cross- multiply )
( cross- multiply )
2x = 6 ( divide both sides by 2 )
x = 3