Question

A 63.9 kg water skier is pulled by a

125 N force at a 31.5° angle, while
the water creates a 84.8 N force
pulling directly backward. What is the
y-component of the acceleration?

Answer 1

\: \\ a_(y) = 1.02 \: \frac{m}{ {s}^(2) } \: "y \: component \: of \: acceleration" " src="
`image`

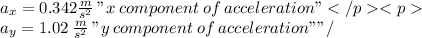
Step-by-step explanation:

Given a mass of 63.9kg with a total applied force of 125 N at a 31.5° inclination relative to the horizontal and vertical, and a horizontal resistance force of 84.8 N. The components of acceleration can be calculated as follows:

Force = mass × acceleration

Vertical component of a vector = vector × Sin(angle)

Horizontal component of a vector = vector × Cos(angle)

extra:

V = √x^2+y^2

θ (angle, "theta") = arctan or inverse tan(y/x) (For this instance. Theta is usually an angle measure though)

x = V cos θ

y = V sin θ

____________________

To find the vertical component of acceleration we must first take the vector quantity of our force which is 125 N (Newtons) and it's angle of 31.5°.

Vertical force = 125 × sin(31.5 degrees) = 125 × 0.5225 = 65.312 N [aka the normal force]

This works because force is a vector, it has both direction(by the angle of force), and magnitude(it's quantity).

Then take the force equation, and rearrange it to solve for the upward acceleration: F = m × a → a = F/m.

a = 65.312/63.9 ≈ 1.02 m/s^2.

Then for the horizontal acceleration, take the cosine for the horizontal part