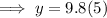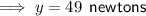Question

The gravitational force ona abody falling towards the earthb is directly proportional to the mass of the body the gravitiaional force on the body js 2 kg is 19.6 newtons

A. Write a direct variation equation relating the mass x and the gravitational force y on the falling body


B. Using your equation from 4.a find the gravitaional force of an object with the mass of 5kg

Don't RIP OFF OR I WILL REPORT

Answer 1

A. y = 9.8x

B. 49 newtons

Explanation:

Part A

Definition of the given variables:

• x = mass in kg
• y = gravitational force in newtons

If the gravitational force is directly proportional to the mass, then:

`y \propto x \implies y=kx \quad \textsf{(for some constant k)}`

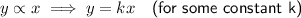
Given:

• x = 2 kg
• y = 19.6 newtons

Substitute the given values into the equation and solve for k:

`\implies 19.6=2k`

`\implies k = 9.8`

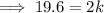
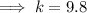
Therefore, the direct variation equation is:
`y=9.8x`

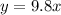
Part B

To find the gravitational force of an object with mass of 5 kg, substitute x = 5 into the found equation from part A and solve for y:

`\implies y=9.8(5)`

`\implies y=49\:\: \sf newtons`

Answer 2

• A. y = 9.8x
• B. 49 Newtons

Explanation:

Direct proportional relationship formula

• y = kx, where y- dependent variable, x- independent variable, k- coefficient of proportionality

Given values

• x = 2 kg
• y = 19.6 N

Find the value of k using the formula

• 19.6 = 2k
• k = 19.6/2
• k = 9.8

Part A

The equation for this case is

• y = 9.8x

Part B

Find the value of y when x = 5

• y = 9.8*5 = 49 N