Question

PLEASE HELP URGENT!!!!!!

The sum of 3 numbers is 145. Seven times the second number is twice the first number and twice the second number is six times the third number.

Write the new ratio of the three numbers if the second number doubles and the third number is increased by one less than one fifth of the first number.

Answer 1

`7:4:2`

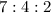
Explanation:

Assign variables for the 3 numbers. Let the first number be x, the second number be y, and the third number be z.

"The sum of the 3 numbers is 145", therefore:

• 
  `x+y+z=145`
  `\text{Equation I}`

"Seven times the second number is twice the first number":

• 
  `7y=2x`
  `\text{Equation II}`

"Twice the second number is six times the third number":

• 
  `2y=6z`
  `\text{Equation III}`

We can solve for x, y and z using this system of equations. Let's solve for y in the first equation by putting the other variables in terms of y in Equations II and III.

Solve for x in
`\text{Equation II}`:

• 
  `x=(7)/(2)y`

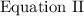Solve for z in
`\text{Equation III}`:

• 
  `z=(2)/(6) y= (1)/(3) y`

Substitute these values into
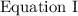`\text{Equation I}` to solve for y.

• 
  `(7)/(2) y+y+(1)/(3) y=145`

Combine like terms using common denominators. The least common denominator is 6. Multiply
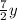`(7)/(2) y` by
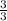`(3)/(3)`, multiply
`y` by
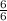`(6)/(6)`, and multiply
`(1)/(3) y` by
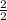`(2)/(2)` to make all of the denominators = 6.

• 
  `((3)/(3))(7)/(2) y +((6)/(6))y+((2)/(2))(1)/(3) y=145`

• 
  `(21)/(6)y + (6)/(6)y + (2)/(6)y=145`

Add the fractions together.

• 
  `(29)/(6)y=145`

Solve for y by multiplying both sides by
`(6)/(29)`.

• 
  `y=145((6)/(29) )= (870)/(29) =30`

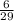We have found that y = 30. Now we can use this known value in order to solve for both x and z in Equations II and III.

`\text{Equation II}:`

• 
  `7y=2x`

• 
  `7(30)=2x`
• 
  `210=2x`
• 
  `105=x`
• 
  `x=105`

`\text{Equation III}:`

• 
  `2y=6z`
• 
  `2(30)=6z`
• 
  `60=6z`
• 
  `10=z`
• 
  `z=10`

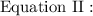
We have found that x = 105, y = 30, and z = 10. Now we can write the new ratio of these 3 numbers:

"Write the new ratio of the three numbers if the second number doubles and the third number is increased by one less than one fifth of the first number":

• 
  `2y`
• 
  `z+ ((1)/(5) x-1)`

The question asks for the new ratio once we evaluate these expressions. The variable x is the only one that stays the same at the end: 105.

• 
  `2(30)=60`
• 
  `(10)+[(1)/(5) (105)-1 ]\\ (10) + (21-1 )\\ (10)+(20)=30`

Our final numbers are x = 105, y = 60, and z = 30. We can create the ratio between these numbers by fully simplifying them. Right now we have
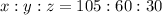`x:y:z=105:60:30`. Start by dividing all of the numbers by 5.

We get
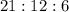`21:12:6`. This ratio can be simplified further by dividing all of the numbers by 3. We then get the ratio of:
`7:4:2`.

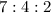This ratio cannot be simplified any further, therefore, it is the new ratio of the three numbers.