Question

the difference between the squares of two numbers is 5. four times the square of the first number increased by the square of the second number is 40. find the numbers.

Answer 1

The first number is
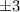`\pm 3` and the second number is
`\pm 2`.

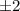Explanation:

Create two equations using the given information. Let's set variables for the two numbers as x and y.

"The difference between the squares of two numbers is 5":

• 
  `x^2-y^2=5`

We can let x be the first number;

"Four times the square of the first number increased by the square of the second number is 40":

• 
  `4x^2 + y^2 =40`

Now we have a system of equations that we can solve for x and y:

• 
  `x^2-y^2=5`
• 
  `4x^2 + y^2 =40`

It looks like
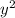`y^2` can easily be canceled out from both equations if we use the elimination method. Add these equations together.

• 
  `5x^2=45`

Divide both sides of the equation by 5.

• 
  `x^2=9`

Take the square root of both sides of the equation.

• 
  `x= \pm3`

It doesn't matter if we use positive or negative 3, since the variables x and y are both being squared, so the outcome will always be positive.

Substitute either positive or negative 3 into the first equation.

• 
  `(3)^2-y^2=5`

Evaluate the exponent.

• 
  `9-y^2=5`

Subtract 9 from both sides of the equation.

• 
  `-y^2=-4`

Divide both sides of the equation by -1 to get rid of the negative sign in front of
`y^2`.

• 
  `y^2=4`

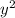Square root both sides of the equation.

• 
  `y= \pm2`

Again, it doesn't matter if y is positive or negative since it is getting squared regardless.

The first number is
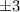`\pm 3` and the second number is
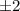`\pm 2`.

• 
  `x= \pm3`
• 
  `y= \pm2`