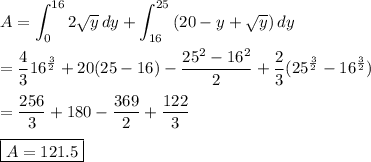Question

Y = x^2
y = 20 − x
Find the area of the region by integrating with respect to y.

Answer 1

9514 1404 393

Answer:

121.5

Explanation:

The region of integration appears to be that area bounded by the parabola and the line. The line intersects the parabola at (-5, 25) and (4, 16).

Integrating in the y-direction requires the region be divided into two parts. One part is for y-values between 0 and 16, where the differential of area is bounded by the parabola on both ends. The other part is for y-values between 16 and 25, where the line is one boundary and the parabola is the other. Then the integral is ...

`\displaystyle A=\int_0^(16){2√(y)}\,dy+\int_(16)^(25){(20-y+√(y))}\,dy\\\\=(4)/(3)16^{(3)/(2)}+20(25-16)-(25^2-16^2)/(2)+(2)/(3)(25^{(3)/(2)}-16^{(3)/(2)})\\\\=(256)/(3)+180-(369)/(2)+(122)/(3)\\\\\boxed{A=121.5}`