Question

Enter the exponential decay function using t (for time) as the independent variable to

model the situation. Select the graph of the function. Enter the function's domain and
range. Then complete the explanation of what the y-intercept represents in the context of
the problem. If necessary, round to the nearest penny.
The value of a couch is decreasing at a rate of 6.3% per year. In 2007, the couch was worth
$1,232. Find the value of the couch in 2014.

Answer 1

The decay function is
`y(t)=a(1-r)^(t)`

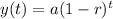
The graph is attached down

The domain is {t: t ≥ 0}

The range is {y: y > 0}

The y-intercept represents the initial value of the couch

The value of the couch in 2014 is $781.25 to the nearest penny

Explanation:

The form of the decreasing exponential function is
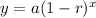`y=a(1-r)^(x)`, where

• a is the y-intercept ⇒ initial amount

• r is the rate of in decimal

• y is the dependent amount

• x is the independent amount

∵ The value of a couch is decreasing at a rate of 6.3% per year

∴
`y(t)=a(1-r)^(t)`

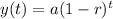
∴ y represents the amount of money

∴ t represents the number of years

∴ r = 6.3% = 6.3/100 = 0.063

∵ In 2007, the couch was worth $1,232

∴ The initial value is $1,232

∴ a = 1,232

∵ We need to find the value of the couch in 2014

∴ t = 2014 - 2007 = 7 years

→ Substitute the values of a, r, and t in the function above

∵ The decay function is
`y(t)=1,232(1-0.063)^(t)`

∵
`y(7)=1,232(1-0.063)^(7)`

∴
`y(7)=1,232(0.937)^(7)`

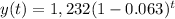
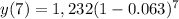
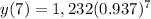
∴ y(7) = 781.2460671

→ Round it to the nearest penny (2 d.p)

∴ y(7) = 781.25

∴ The value of the couch in 2014 is $781.25 to the nearest penny

∵ The y-intercept is the value of y at t = 0

∴ The y-intercept represents the initial value of the couch

→ The graph is attached down

→ The domain is {t: t ≥ 0}

→ The range is {y: y > 0}