Question

Ayden spent 35 minutes studying for his math test. He scored a 72%. Olivia spent 75 minutes studying, and scored a 97%. Assume there is a linear relationship between these two quantities. Write an equation to represent the score a student got on the test as a function of the amount of time spent studying.

Answer 1

s = 0.625t + 50.125

Explanation:

Let the equation that represents the relation between the time of study and marks obtained is,

s = mt + b

Here 's' = marks scored by the students

m = marks obtained by the study per minute

t = duration of study

b = marks obtained without study

Slope of the line having points
`(x_1,y_1)` and
`(x_2,y_2)` is given by,

m =
`(y_2-y_1)/(x_2-x_1)`

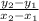
Slope of the line passing through two points (35, 72) and (75, 97)

m =
`(97-72)/(75-35)`

m =
`(25)/(40)`

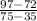
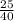
m = 0.625

Equation of the line will be,

y = 0.625t + b

Since this line passes through (35, 72),

72 = 0.625(35) + b

b = 72 - 21.875

b = 50.125

Therefore, equation representing duration of study and the score obtained will be,

s = 0.625t + 50.125