Question

For the following, determine the value of the discriminant and hence sketch the parabola using the most efficient approach. Label all intercepts and the vertex.

y=25x^2 −30x+9

Answer 1

discriminant(∆) = 0

vertex and intercept labeled on the graph below

NOTE: the x-intercept is the vertex

Explanation:

Comparing
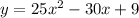`y = 25x^(2) - 30x + 9` with
`y = ax^(2) − bx + c`

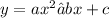
Thus,

a=25 b = -30 and c = 9

`discriminate (d) = b^(2) - 4ac\\d = (-30)^(2) - 4(25)(9)\\`

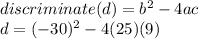
the ' - ' when squared becomes '+'

d = 900 - 900

d = 0

Thus, the value of discriminant(∆) is 0