Answer:
Brooklyn's method results in more money after 2 years
Explanation:
Compound Interest Formula
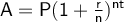
where:
- A = final amount
- P = principal amount
- r = interest rate (in decimal form)
- n = number of times interest applied per time period
- t = number of time periods elapsed
Patrick's Method
Given:
- P = $300
- r = 3% = 0.03
- n = 4
- t = 2
Substituting the given values into the formula and solving for A:
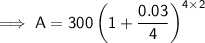
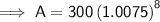
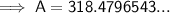
Therefore, using Patrick's method, there would be $318.48 in the account after 2 years.
Brooklyn's Method
Given:
- P = $300
- r = 5% = 0.05
- n = 12
- t = 2
Substituting the given values into the formula and solving for A:
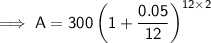
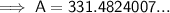
Therefore, using Brooklyn's method, there would be $331.48 in the account after 2 years.
As $331.48 > $318.48 then Brooklyn's method results in more money after 2 years.