Question

Find the value of n for the regular n-gon described.

Each interior angle of the regular n-gon has a measure of 75.2º.

Answer 1

n = 3.44

Explanation:

The interior angle of a regular n-gon is given by the formula;

`I = \frac {180(n-2)}{n}`

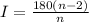
Where,

• I represents the interior angle.

• n represents the number of sides.

Given that interior angle = 75.2°

Substituting into the equation, we have;

`75.2 = \frac {180(n-2)}{n}`

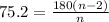
Cross multiplying, we have;

`75.2n = 180(n-2)`

`75.2n = 180n - 360`

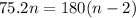
Rearranging the equation, we have;

`180n - 75.2n = 360`

`104.8n = 360`

`n = \frac {360}{104.8}`

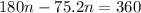
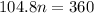
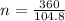
n = 3.44

Therefore, the number of sides "n" of the regular n-gon described is 3.44.