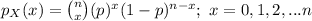Question

A binomial probability experiment is conducted with the given parameters. Compute the probability of x successes in the n independent trials of the experiment.

Answer 1

The probability mass function of X is:

`p_(X)(x)={n\choose x}(p)^(x)(1-p)^(n-x);\ x=0,1,2,...n`

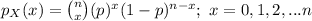
Explanation:

A Binomial experiment has the following properties:

• There are a fixed number of trials (n).

• Each trial are independent of the others.

• Each trial has only two outcomes: Success and Failure

• Each trial has the same probability of success (p).

If a random variable X is used in an experiment and the experiment has all the above mentioned properties, then the random variable X is known as a binomial random variable.

Then the probability mass function of X is known as binomial probability distribution.

The probability mass function of X is:

`p_(X)(x)={n\choose x}(p)^(x)(1-p)^(n-x);\ x=0,1,2,...n`