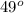Question

If m\displaystyle \angle∠F = (6x + 7) and m\displaystyle \angle∠H = (9x - 14), then solve for m\displaystyle \angle∠F if the two angles are Alternate Interior Angles.

Answer 1

m<F =
`49^(o)`

Explanation:

Alternate interior angles have equal values. So that;

m<F = m<H

Given that: m<F = (6x + 7) and m<H = (9x - 14).

Then,

(6x + 7) = (9x - 14)

6x + 7 = 9x - 14

collecting like terms, we have

6x - 9x = -7 - 14

-3x = -21

3x = 21

Divide both sides by 3, to have;

x =
`(21)/(3)`

= 7

therefore,

m<F = (6x + 7)

= 6 x 7 + 7

= 42 + 7

=
`49^(o)`

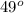
m<H = (9x - 14)

= 9 x 7 - 14

= 63 - 14

=
`49^(o)`