Question

Laura corto un trozo de tela cuadrada para un mantel. Luego se dio cuenta de que ese trozo no alcanzava a cubrir la superficie pues, había un error de medidas. Pará arreglarlo le agrego dos prendas haciendo el el mantel ahora sea rectangular, su largo mide 50 cm mas y su ancho 3o cm más que las medidas del mantel original. Si el nuevo mantel cubre 16800 cm2 ¿cuál es la medida del lado del primer mantel y cuantos cm2 cubría?

Answer 1

La medida del lado del primer mantel es 90 centímetros.

Primer mantel cubría un área de 8100 centímetros cuadrados.

Explanation:

Sea
`x` la longitud del lado del mantel original, cuya forma es cuadrada y está medida en centímetros. Al agregarse dos prendas, se obtiene un rectángulo, cuya área (
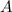`A`), medida en centímetros cuadrados, se halla mediante la siguiente fórmula:

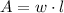`A = w\cdot l` (Eq. 1)

Donde:

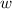`w` - Ancho, medido en centímetros.

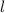`l` - Largo, medido en centímetros.

Si
`A = 16800\,cm^(2)`,
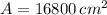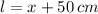`l = x+50\,cm` y
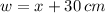`w = x+30\,cm`, tenemos el siguiente polinomio de segundo orden:

`16800 = (x+50)\cdot (x+30)`

`16800 = x^(2)+80\cdot x +1500`

`x^(2)+80\cdot x -15300 = 0`

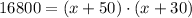
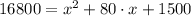
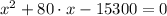
Por la fórmula de la Cuadrática tenemos que las raíces del polinomio son:

`x_(1) = 90\,cm`,
`x_(2) = -170\,cm`.

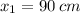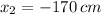Solamente la primera raíz es una solución físicamente razonable. Entonces, la medida del lado del primer mantel es 90 centímetros.

Ahora, el área del primer mantel es:

`A = (90\,cm)^(2)`

`A = 8100\,cm^(2)`

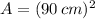
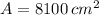
Primer mantel cubría un área de 8100 centímetros cuadrados.