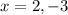Question

How many different roots does the polynomial function have y = (x-2)(x+3)^2 have

Answer 1

`x=2,-3`

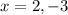
Explanation:

Set
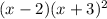`(x-2)(x+3)^2` equal to
`0`.

`(x-2)(x-3)^22=0`

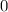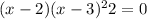
Solve for
`x`.

If any individual factor on the left side of the equation is equal to
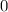`0`, the entire expression will be equal to
`0`.

`x-2=0\\(x+3)^2=0`

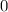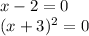
Set the first factor equal to
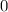`0` and solve.

Set the first factor equal to
`0`.

`x-2=0`

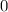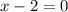
Add
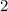`2` to both sides of the equation.

`x=2`

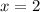
Set the next factor equal to
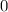`0` and solve.

Set the next factor equal to
`0`.

`(x+3)^2=0`

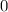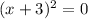
Set the
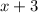`x+3` equal to
`0.`

`x+3=0`

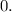
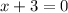
Subtract
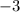`-3` from both sides of the equation.

`x=-3`

The final solution is all the values that make
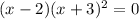`(x-2)(x+3)^2=0` true.

`x=2,-3`