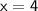Answer:
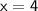
Explanation:
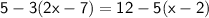
To get rid of the parentheses, we'll apply the distributive property. Staring with the left side, multiply -3 by (2x-7).
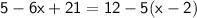
5+ 21= 26
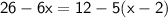
Now, let's do the same thing to the right side. Multiply -5 by (x-2) »12−5x+10, than add 12+ 10 = 22 .
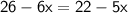
Combine like terms.
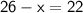
Subtract 26 from both sides.
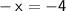
Multiply both sides by -1.