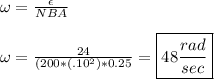Question

a simple generator has 200 loop square coil 10 cm on a side .how fast must it turn in a 0.25 T field to produce 24v peak out put​

Answer 1

Hi there!

Recall Faraday's Law:

`\epsilon = N(d\Phi_B)/(dt)`

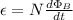
ε = Emf (V)
N = Number of loops

ΦB = Magnetic Flux (Wb)
t = time (s)

Since the magnetic field is constant, we can take this out of the time derivative:

`(d\Phi_B)/(dt) = B * (dA)/(dt)`

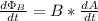
Therefore:

`\epsilon = N B (dA)/(dt)`

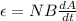
We can express 'A', the area in which the magnetic field passes as:

`A = Acos(\omega t)`

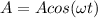
Taking the time derivative:

`(dA)/(dt) = A\omega sin(\omega t)`

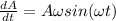
ω = angular speed of coil (rad/sec)

Now, combine with the above expression:

`\epsilon = NBA\omega sin(\omega t)`

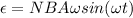
The maximum output will occur when the loop's area vector is PERPENDICULAR to the field, so sin(ωt) = 1.

Therefore:

`\epsilon = NBA\omega \\\\`

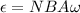
Rearrange to solve for ω:

`\omega = (\epsilon)/(NBA)\\\\\omega = (24)/((200 * (.10^2) * 0.25) = \boxed{48 (rad)/(sec)}`