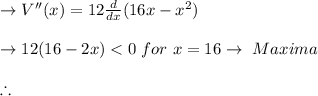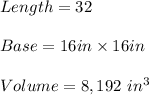Question

A country's postal service will accept a package if its length plus its girth (the distance all the way around) does not exceed 96 inches. Find the dimensions and volume of the largest package with a square base that can be mailed. length in base in × in volume in3

Answer 1

Following are the solution to the given point:

Explanation:

Let the box length l and the square base side be x, then

`\to l+4x= 96 \\\\\to l=96-4x`

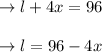
Calculating the volume of the box is:

`\to V (x) = x^2 \\\\ \to l = x^2(96-4x)`

To find the critical value in this way, distinguish V with x and equal to zero

`\to V'(x)=0 \\\\\to 4 (d)/(dx)(24x^2 - x^3)=0\\\\\to 4 (48x- 3x^2)=0\\\\\to 12x(16-x) = 0\\\\\to x= 12... [x \\eq 0]` (because the box will not exists)

Find the second derivative for maximum / minimum control as:

`\to V''(x)= 12 (d)/(dx) (16x-x^2) \\\\\to 12 (16 -2x) < 0 \ for \ x = 16 \to \ Maxima \\\\\therefore`

`Length = 32 \\\\Base = 16 in * 16 in \\\\Volume= 8,192 \ in^3`