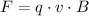Question

g First find the magnitude of the force F on a positive charge q in the case that the velocity v⃗ (of magnitude v) and the magnetic field B⃗ (of magnitude B) are perpendicular. Express your answer in terms of v, q, B, and other quantities given in the problem statement.

Answer 1

The magnitude of the force F on a positive charge q in the case that the velocity v and the magnetic field B are perpendicular is
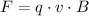`F = q\cdot v\cdot B`, measured in newtons.

Step-by-step explanation:

From classical theory on Magnetism, the vectorial form of the magnetic force on a particle is given by:

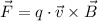`\vec F = q\cdot \vec v * \vec B` (Eq. 1)

Where:

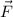`\vec F` - Magnetic force, measured in newtons.

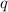`q` - Electric charge, measured in coulombs.

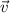`\vec v` - Velocity of the particle, measured in meters per second.

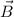`\vec B` - Magnetic field, measured in tesla.

By definition of cross product, we get that magnitude of magnetic force on a positive charge
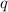`q` is:

`F = q\cdot v\cdot B \cdot \sin \theta` (Eq. 2)

Where:

`v` - Speed of the particle, measured in meters per second.

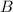`B` - Magnitude of the magnetic field, measured in tesla.

`\theta` - Angle between the velocity of the particle and magnetic field, measured in sexagesimal degrees.

If velocity and magnetic field are perpendicular, then (Eq. 2) is reduced into this form: (
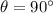`\theta = 90^(\circ)`)

`F = q\cdot v\cdot B`