Complete Question
Newly purchased automobile tires of a certain type are supposed to be filled to a pressure of 30 psi. Let μ denote the true average pressure. Find the P-value associated with each of the following given z statistic values for testing H0: μ = 30 versus Ha: μ 30 when σ is known. (Give the answers to four decimal places.)
calculate for each
(a) z = 2.30
(b) z = -1.7
Answer:
a
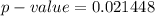
b

Step-by-step explanation:
From the question we are told that
The population mean is
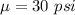
The null hypothesis

The alternative hypothesis is
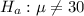
Considering question a
Here the test statistics is (a) z = 2.30
From the z table the probability of (Z > 2.30) is
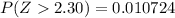
Generally the p-value is mathematically represented as
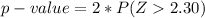
=>
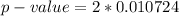
=>
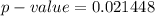
Considering question b
Here the test statistics is (a) z = -1.7
From the z table the probability of (Z < -1.7) is
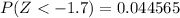
Generally the p-value is mathematically represented as

=>
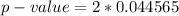
=>
