Question

A certain brand of laundry detergent comes in two sizes. The smaller size is 24 oz and cost $3.99. The larger size is 64 oz and cost $6.99. Which has the lower unit cost?

Answer 1

Given:

The smaller size is 24 oz and cost $3.99.

The larger size is 64 oz and cost $6.99.

To find:

Which has the lower unit cost?

Solution:

The formula for unit cost is

`\text{Unit cost}=\frac{\text{Total cost}}{\text{Quantity}}`

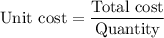
The unit cost of smaller size is

`\text{Unit cost of smaller size}=(3.99)/(24)`

`\text{Unit cost of smaller size}=0.16625`

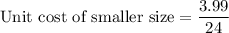
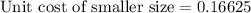
The unit cost of larger size is

`\text{Unit cost of larger size}=(6.99)/(64)`

`\text{Unit cost of larger size}=0.10922`

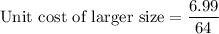
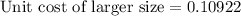
It is clear that, 0.10922 is less than 0.16625.

Therefore, the unit cost of larger size is lower.