Question

The number of different simple random samples of size 5 that can be selected from a population of size 8 is

Answer 1

Number of different simple random samples of size 5 that can be selected from a population of size 8 = 56 ways

Explanation:

Step 1: Stating the combination formula

The number of selections of a number n, taking r at a time is given by the formula:
`(n!)/((n - r!)r!)`

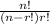
From the formula above, n is population size = 8

r is sample size = 5

Step 2: Substituting the values of n and r

Number of possible selections = 8!/(8 -5)*5! = 8!/3! * 5!

Number of possible selections =
`(8*7*6*5*4*3*2*1)/(3*2*1 * 5*4*3*2*1)`

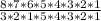
Number of possible selections = 56

Therefore, number of different simple random samples of size 5 that can be selected from a population of size 8 = 56 ways