Question

An ice skater has a moment of inertia of 5.0 kg.M^2 when her arms are outstretched , and at the time she is spinning at 3.0 rev/s . If she pulls in her arms and decreases her moment of inertia to 2.0 kg.M^2 , how fast will she be spinning

Answer 1

The ice skater will spin at an angular speed of 7.5 revolutions per second.

Step-by-step explanation:

From statement we notice that ice skater can be considered as a system, on which no external forces are exerted, such that Principle of Angular Momentum can be applied:

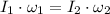`I_(1)\cdot \omega_(1) = I_(2)\cdot \omega_(2)` (Eq. 1)

Where:

`I_(1)` - Moment of inertia of the ice skater when her arms are outstretched, measured in kilogram-square meters.

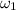`\omega_(1)` - Angular speed when arms are outstretched, measured in revolutions per second.

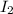`I_(2)` - Moment of inertial of the ice skater when her arms are pulled, measured in kilogram-square meters.

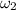`\omega_(2)` - Angular speed when arms are pulled, measured in revolutions per second.

If
`I_(1) = 5\,kg\cdot m^(2)`,
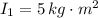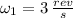`\omega_(1) = 3\,(rev)/(s)` and
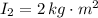`I_(2) = 2\,kg\cdot m^(2)`, the angular speed when arms are pulled is:

`\omega_(2) = (I_(1))/(I_(2)) \cdot \omega_(1)`

`\omega_(2) = \left((5\,kg\cdot m^(2))/(2\,kg\cdot m^(2)) \right)\cdot \left(3\,(rev)/(s) \right)`

`\omega_(2) = 7.5\,(rev)/(s)`

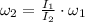
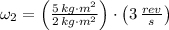
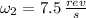
The ice skater will spin at an angular speed of 7.5 revolutions per second.