Answer:
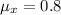
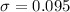
The shape of this sampling distribution is approximately normal
Explanation:
From the question we are told that
The population proportion is
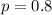
The sample size is n = 100
Generally the expected value of this sampling distribution is mathematically represented as

Generally the standard deviation of this sampling distribution is mathematically represented as

=>
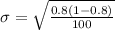
=>
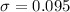
Generally given that the sample is large (i.e n > 30 ) and the standard deviation is finite then the shape of this sampling distribution is approximately normal