Answer: The required probability = 0.8926
Explanation:
Given:
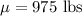 ,
,
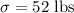
Let x = weight of horse stable.
Sample size : n= 31
Then, the probability that the mean weight of the sample of horses would differ from the population mean by less than 15 will be:
![P(-15<P(\overline{x}-\mu)<15)=P((-15)/((52)/(√(31)))<\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(15)/((52)/(√(31))))\\\\=P(-1.61<z<1.61)\ \ \ [z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}]\\\\=2(z<1.61)-1\ \ \ [P(-z<Z<z)=2(Z<z)-1]\\\\=2( 0.9463)-1\\\\=0.8926](https://img.qammunity.org/2021/formulas/mathematics/college/68eq23m1r5j4ypvxp1y5luj8i67aok7aaa.png)
Hence, the required probability = 0.8926