Question

Given: Triangle ABC is right isosceles. X is the

midpoint of AC. AB = BC
Prove: Triangle AXB is isosceles.

Answer 1

Explanation:

From the figure attached,

Point X is the midpoint of line AC.

Since coordinates of the midpoint of the segment joining endpoints
`(x_1,y_1)` and
`(x_2,y_2)` is given by,

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

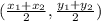
Therefore, coordinates of the point X will be,

=
`((0+2a)/(2),(2a+0)/(2))`

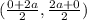
= (a, a)

From triangle AXB,

Length of AB = 2a

Length of AX =
`√((a-0)^2+(a-2a)^2)`

=
`a√(2)`

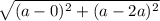
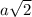
Length of BX =
`√((a-0)^2+(a-0)^2)`

=
`a√(2)`

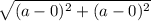
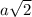
Length of AX = BX =
`a√(2)`

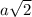
Therefore, triangle AXB is an isosceles triangle.