Question

Et $a_1, a_2, a_3,\dots$ be an arithmetic sequence.

if $a_1 + a_3 + a_5 = -12$ and $a_1a_3a_5 = 80$, find all possible values of $a_{10}$.

Answer 1

Since it's an arithmetic sequence,

`a_2 = a_1 + d`

`a_3 = a_2 + d = a_1 + 2d`

`a_4 = a_3 + d = a_1 + 3d`

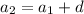
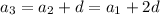
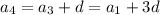
and so on, up to

`a_n = a_1 + (n-1)d`

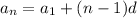
Now, by substitution,

`a_1 + a_3 + a_5 = -12`

`a_1 + (a_1+2d) + (a_1+4d) = -12`

`3a_1 + 6d = -12`

`a_1 + 2d = -4`

`\implies a_1 = -4-2d, a_3 = -4, a_5 = -4+2d`

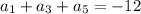
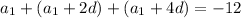
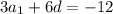
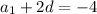
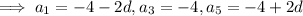
Then the product
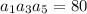`a_1a_3a_5=80` depends only on d, so that

`(-4-2d) * (-4) * (-4+2d) = 80`

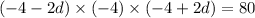
Solve for d :

`(4+2d) (4-2d) = -20`

`16 - 4d^2 = -20`

`4d^2 = 36`

`d^2 = 9`

`d = \pm3`

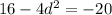
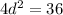
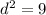
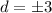
If d = 3, then the first term in the sequence is
`a_1 = -10`, and the tenth term would be
`a_(10) = \boxed{17}`.

If d = -3, then the first term would instead by
`a_1 = 2`, and the tenth term would be
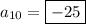`a_(10) = \boxed{-25}`.