Answer:
The coordinates of R' are
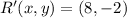 .
.
Explanation:
According to Linear Algebra, dilation consist in expanding a given vector with respect to one of its endpoints by a scalar. That is:
![R'(x, y) = C(x,y) + k\cdot [R(x,y)-C(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/rykid53u6rnsm2o57c1stz9j2sh08162wc.png) (Eq. 1)
(Eq. 1)
Where:
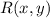 - Original location with respect to origin, dimensionless.
- Original location with respect to origin, dimensionless.
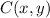 - Point of reference with respect to origin, dimensionless.
- Point of reference with respect to origin, dimensionless.
 - Dilation factor, dimensionless.
- Dilation factor, dimensionless.
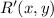 - Dilated point with respect to origin, dimensionless.
- Dilated point with respect to origin, dimensionless.
If we know that
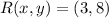 ,
,
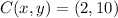 and
and
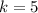 , then the dilated point is:
, then the dilated point is:
![R'(x,y) = (3,8) +5\cdot [(3,8)-(2,10)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/y6hkx1crtai46rxaebawlgfwhamkzk9msp.png)

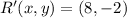
The coordinates of R' are
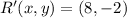 .
.