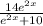Question

Find the indefinite integral using the substitution provided.


`\int\limits({(14e^2^x)/(e^2^x+10)) } \, dx`

`u=e^2^x+10`

Answer 1

Answer:
`7\text{Ln}\left(e^(2x)+10\right)+C`

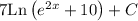
This is the same as writing 7*Ln( e^(2x) + 10) + C

=======================================================

Step-by-step explanation:

Start with the equation
`u = e^(2x)+10`

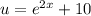
Apply the derivative and multiply both sides by 7 like so

`u = e^(2x)+10\\\\(du)/(dx) = 2e^(2x)\\\\7(du)/(dx) = 7*2e^(2x)\\\\7(du)/(dx) = 14e^(2x)\\\\7du = 14e^(2x)dx\\\\`

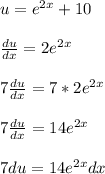
The "multiply both sides by 7" operation was done to turn the 2e^(2x) into 14e^(2x)

This way we can do the following substitutions:

`\displaystyle \int (14e^(2x))/(e^(2x)+10)dx\\\\\\\displaystyle \int (1)/(e^(2x)+10)14e^(2x)dx\\\\\\\displaystyle \int (1)/(u)7du\\\\\\\displaystyle 7\int (1)/(u)du\\\\\\`

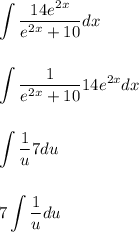
Integrating leads to

`\displaystyle 7\int (1)/(u)du\\\\\\7\text{Ln}\left(u\right)+C\\\\\\7\text{Ln}\left(e^(2x)+10\right)+C\\\\\\`

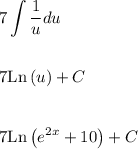
Be sure to replace 'u' with e^(2x)+10 since it's likely your teacher wants a function in terms of x. Also, do not forget to have the plus C at the end. This is a common mistake many students forget to do.

To verify the answer, you can apply the derivative to it and you should get back to the original integrand of
`(14e^(2x))/(e^(2x)+10)`