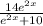Answer:
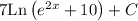
This is the same as writing 7*Ln( e^(2x) + 10) + C
=======================================================
Step-by-step explanation:
Start with the equation
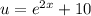
Apply the derivative and multiply both sides by 7 like so
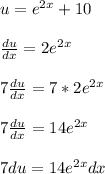
The "multiply both sides by 7" operation was done to turn the 2e^(2x) into 14e^(2x)
This way we can do the following substitutions:
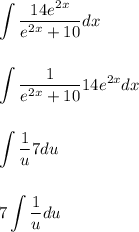
Integrating leads to
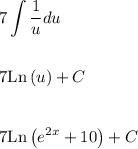
Be sure to replace 'u' with e^(2x)+10 since it's likely your teacher wants a function in terms of x. Also, do not forget to have the plus C at the end. This is a common mistake many students forget to do.
To verify the answer, you can apply the derivative to it and you should get back to the original integrand of