Question

A sheet of BCC iron 1.5-mm thick was exposed to a carburizing atmosphere on one side and an carburizing atmosphere on the other side at 725°C. After having reached steady state, the iron was quickly cooled to room temperature. The carbon concentrations at the two surfaces were determined to be 0.012 and 0.0069 wt%. Calculate the diffusion coefficient if the diffusion flux is 3.6 × 10-8 kg/m2-s, given that the densities of carbon and iron are 2.25 and 7.87 g/cm3, respectively.

Answer 1

Diffusion coefficient D = 2.6613 × 10⁻¹¹ m²/s

Step-by-step explanation:

From the given information:

Carbon concentration
`C_c` = 0.012

Iron concentration
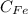`C_(Fe)` = 100 - 0.012 = 99.988

Density of carbon = 2.25 g/cm³

Density of iron = 7.87 g/cm³

We can convert the carbon concentrations from weight percentage to kilograms carbon per meter cubed by using the formula.

`C^*_c = (C_c)/((C_c)/(\rho_c)+(C_(Fe))/(\rho_(Fe)))* 10^3`

`C^*_c = (0.012)/((0.012)/(2.25 \ g/cm^3)+(99.988)/(7.87 \ g/cm^3))* 10^3`

`C^*_c = (0.012)/(0.00533 \ g/cm^3 + 12.71 \ g/cm^3) * 10^3`

`C^*_c = 0.9437 \ kgC/m^3`

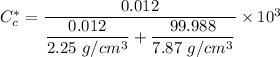
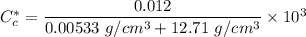
However; for 0.0069 wt% C

`C^*_c = (C_c)/((C_c)/(\rho_c)+(C_(Fe))/(\rho_(Fe)))* 10^3`

`C^*_c = (0.0069)/((0.0069)/(2.25 \ g/cm^3)+(99.9931)/(7.87 \ g/cm^3))* 10^3`

`C^*_c =0.5429 \ kgC/m^3`

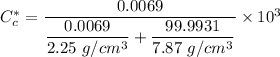
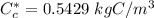
Thus; the diffusion coefficient can be computed by using the formula:

`D = - J \begin {bmatrix} (x_A-x_B)/(C_A-C_B)\end {bmatrix}`

`D = - (3.6 * 10^(-8) \ kg/m^2-s) \begin {bmatrix} (-15^(-3) \ m )/(0.9437 \ kgC/m^3 - 0.5429 \ kgC/m^3)\end {bmatrix}`

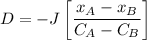
D = 2.6613 × 10⁻¹¹ m²/s