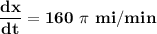Question

4. (10 points)A lighthouse is located on a small island 4 mi away from the nearest point P on a straight shoreline and its light makes ten revolutions per minute. How fast (in mi/min) is the beam of light moving along the shoreline when it is 4 mi from P

Answer 1

The beam of the light is moving along the shoreline at the rate of
`\mathbf{ 160 \ \pi \ mi/min}`

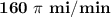
Explanation:

From the given information: Let say x is the distance between the lighthouse and the shoreline. Then, the tangent of trigonometry can be written as:

`tan (\theta )=(x)/(4)`

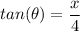
In respect to time, the expression can be derived as:

`sec^2 (\theta) (d \theta)/(dt) = (1 )/(4)(dx)/(dt)`

`(dx)/(dt)=(4)/(cos ^2 (\theta) )(d \theta)/(dt)`

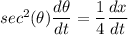
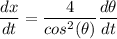
To estimate the value of
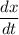`(dx)/(dt)`, we need to know cos²(θ) and D

where;

D =
`√(4^2+4^2)= √(32)\ mi`

`cos (\theta) = (4)/(D)`

`cos (\theta) = (4)/(√(32))`

`cos (\theta) = (4)/(√(16 * 2))`

`cos (\theta) = (4)/(4 √(\ 2))`

`cos (\theta) = (1)/( √(\ 2))`

`cos ^2 (\theta)= (1)/(2)`

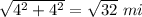
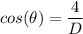
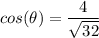
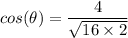
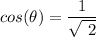
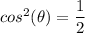
Finally, we substitute the value of
`cos^2(\theta)` and
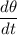`(d \theta)/(dt)` in the expression derived earlier.

i.e.

`(dx)/(dt) = (4)/((1)/(2))* 10 \ rev/min`

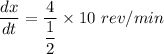
where;

10 rev/min = (10 × 2π) rad/min = 20π rad/min

Then:

`(dx)/(dt) = (4)/((1)/(2))* 20 \ \pi`

`\mathbf{(dx)/(dt) = 160 \ \pi \ mi/min}`