Question

Proof that an invertible function f can have only one inverse

Answer 1

Explanation:

We remeber that If we compose a function and it's inverse,

`f(f {}^( - 1) x) = x`

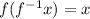
A invertible function is one to one so suppose that we have two inverse, g(x) and h(x). Let plug them in ,

`f(h(x)`

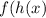
and

`f(g(x)`

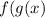
Since f is a invertible function, it is one to one so if g and h are both inverse of f, then they are eqaul

`f(h(x) = f(g(x)`

`h(x) = g(x)`

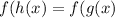
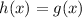
Thus, a invertible function can have only one inverse.