Question

Prove that,
(1+sin theta + cos theta) ^2 = 2(1+sin theta) (1+cos theta) ​

Answer 1

Proof below

Explanation:

Trigonometric Identities

Before we prove the given identity, we need to recall:

`(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc`

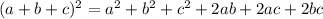
We have to prove that:

`(1+\sin\theta+\cos\theta)^2=2(1+\sin\theta)(1+\cos\theta)`

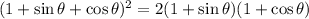
Let's expand the square on the left side as indicated in the formula above:

`(1+\sin\theta+\cos\theta)^2=1^2+\sin^2\theta+\cos^2\theta+2\sin\theta+2\cos\theta+2\sin\theta\cos\theta`

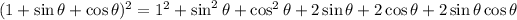
Recall the fundamental trigonometric identity:

`\sin^2\theta+\cos^2\theta=1`

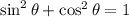
Substituting and operating:

`(1+\sin\theta+\cos\theta)^2=2+2\sin\theta+2\cos\theta+2\sin\theta\cos\theta`

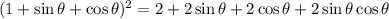
Factoring by 2:

`(1+\sin\theta+\cos\theta)^2=2(1+\sin\theta+\cos\theta+\sin\theta\cos\theta)`

Factoring cos θ in the last two terms:

`(1+\sin\theta+\cos\theta)^2=2[1+\sin\theta+\cos\theta(1+\sin\theta)]`

Factoring
`1+\sin\theta`

`(1+\sin\theta+\cos\theta)^2=2(1+\sin\theta)(1+\cos\theta)`

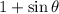
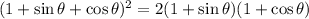
Proven